Weight-Balanced Tree - SML

1. Introduction
2. Inserting a new value
3. Querying for an Element
4. Deleting an Element
5. Appendix: Source Code by Files
- 5.1. ord.sig
- 5.2. wbtree.fun
6. References

1. Introduction

Haskell uses Weight-balanced trees in their implementations of sets (Data.Set) and maps (Data.Map). But their implementation is rather tricky. So I thought I would write some notes about them. We should recall, in general, a binary tree is inductively defined as

A Binary Tree is either

the empty tree
a branch consisting of a value, a left subtree, a right subtree, and possibly some metadata.

Algebraic data types were invented specifically to describe these inductive definitions, we could easily implement a tree in Standard ML as:

type Metadata = (* whatever you want, we omit it *);

datatype 'a BinaryTree
  = EmptyTree
  | Branch of 'a * ('a BinaryTree) * ('a BinaryTree) *  Metadata;

The Branch constructor takes a 4-tuple (value, left_subtree, right_subtree, metadata) and produces a BinaryTree object. (The ordering of the components of the 4-tuple is arbitrary, we could easily make metadata the first component.)

What's so great about using algebraic data types for implementing trees? It helps us reason about the code. Whenever we write a function concerning a BinaryTree object, we can write one clause to handle the case of the empty tree, and another separate clause to handle the case of a branch. For example, we could count the nodes in a tree thusly:

fun node_count EmptyTree = 0
  | node_count (Branch (_, left, right, _))
    = 1 + node_count left + node_count right;

If the tree were ordered such that the left subtree contained all values less than the value of the branch (and the right subtree contained all values greater than the value of the branch), and if further the left and right subtrees were equal in size, then searching for a value would take about \(\log_{2}(n)\) comparisons where \(n\) is the size of the tree. Other operations would similarly take logarithmic time, which is desirable compared to a linked list's linear time.

We can weaken our demand that the left and right subtrees be equal in size to be "neither branch should be horribly bigger than the other" and still have logarithmic runtime for the tree operations.

Let \(\Delta\in\mathbb{R}\) be a positive real constant (called the Weight Ratio) greater than 1.

Then a Weight-balanced tree is a binary tree \(T\), whose metadata is a non-negative real number called the tree's Weight denoted \(W(T)\), such that the left subtree is Balanced with respect to the right subtree (in the sense that one subtree's weights are no larger than some multiple of the weight of the other subtree), specifically: \(\Delta\cdot W(L)\geq W(R)\) and \(\Delta\cdot W(R)\geq W(L)\).

Phrased differently, the tree is balanced if the ratio of weights for the subtrees \(W(L)/W(R)\) and \(W(R)/W(L)\) are not larger than the weight-ratio parameter \(\Delta\) (i.e., \(\Delta\geq W(L)/W(R)\) and \(\Delta\geq W(R)/W(L)\)) provided \(W(R)\neq0\) and \(W(L)\neq0\).

The common convention takes the weight of the tree \(W(T)\) to be its size (i.e., number of nodes) denoted \(|T|\); we will take \(W(T)=1+|T|\) to handle pathological edge-cases with populating an initially empty tree.

Now, we want to implement in Standard ML a weight-balanced tree as an algebraic data type, something like:

(* Wishful thinking: *)
datatype 'a WBTree = Empty
                   | Branch of int * 'a * ('a WBTree) * ('a WBTree);

This doesn't quite work since we want to make the values in tree nodes "comparable", in the sense that they have a specified compare: 'a * 'a -> order function given. We want this so we can enforce the desired condition that the left subtree contains values smaller than the branch node's value (and similarly the right subtree consists of values greater than the branch node's value).

Standard ML's type system is too weak to enforce this demand on its own. But SML's module system let's us guarantee this by making WBTree a functor, i.e., a structure parametrized by an ORDERED module.

1.1. A Word about Style and Conventions

Following the Standard ML Basis Library, we will adopt the naming convention of "naming similar things similarly". So we will test for emptiness using a function named null in a nod to List.null. Sometimes this coincides with Haskell's naming conventions (e.g., Data.Map.null), sometimes it will not.

We will also part from Standard ML when the name is too much of a stretch (e.g., we will talk about the size of a tree, not the length of a tree).

1.2. Ordered Elements

Following Haskell's Data.Ord signature, we will provide a similar ORD signature. Usually it suffices to just define a compare function, then "fill in the gaps"; we thus define a COMPARABLE signature, and then an Ord functor to construct a module with the ORD signature.

The bare minimum we need is just a compare function for a type:

(* ord.sig *)

(* minimal signature which is fleshed out in a functor *)
signature COMPARABLE =
sig
    type t;
    val compare : t * t -> order;
end;

But we will expect an ordered element to have a fuller suite of functions, namely every possible comparison relational operator imaginable, as well as a way to determine which value is max and min:

(* ord.sig *)

signature COMPARABLE = (* ... *);

signature ORD =
sig
    type t;
    val compare : t * t -> order;
    val gt : t * t -> bool;
    val eq : t * t -> bool;
    val lt : t * t -> bool;
    val geq : t * t -> bool;
    val leq : t * t -> bool;
    val max : t * t -> t;
    val min : t * t -> t;
end;

We lastly will have a functor to "hydrate" the ORD signature, given a module implementing COMPARABLE functions:

(* ord.sig *)

signature COMPARABLE = (* ... *);

signature ORD = (* ... *);

functor Ord(Ordered : COMPARABLE) : ORD with type t = Ordered.t =
struct
    type t = Ordered.t;
    val compare = Ordered.compare;
    fun gt (x,y) = compare (x,y) = GREATER;
    fun eq (x,y) = compare (x,y) = EQUAL;
    fun lt (x,y) = compare (x,y) = LESS;
    fun geq (x,y) = not (lt (x,y));
    fun leq (x,y) = not (gt (x,y));
    fun max (x,y) = if lt(x,y) then y else x;
    fun min (x,y) = if lt(x,y) then x else y;
end;

1.3. Initial Functor

We parametrize the WBTree structure by a module abstracting the desired properties of the type for values of the tree. The only desired condition is that it is an ordered type, which in Standard ML is encoded by specifying it is a structure whose signature is ORD:

functor WBTree(Node : ORD) =
struct
  (* more to come *)
end;

A weight-balanced tree is a binary tree with some metadata. For our purposes, the only metadata we track in a branch of a weight-balanced tree is the size of the tree, which is just an int. We abbreviate the constructors for the empty tree as E and a branch of the tree as T. This will be used internally, we will want the rest of the world to only be vaguely aware WBTree.t even exists.

functor WBTree(Node : ORD) =
struct
   (* Declaration for the type of a weight-balanced tree. *)
   datatype t = E
              | T of int * Node.t * t * t;

   (* more to come *)
end;

We also want a "smart constructor" which will automatically track the size of the tree. This may seem silly, but it will preserve the invariant condition size(tree) = 1 + size(left) + size(right) automatically for us. This will be used internally, we will want to avoid making anything outside the functor realize the smart constructor bin even exists.

functor WBTree(Node : ORD) =
struct
   (* Declaration for the type of a weight-balanced tree. *)
   datatype t = E
              | T of int * Node.t * t * t;
   
   (* bin : Node.t -> t -> t -> t *)
   fun bin x l r = T (1 + size l + size r, x, l, r);

   (* more to come *)
end;

Then we flesh out the remaining helper functions for a weight-balanced tree, giving us our initial functor:

(* wbtree.fun *)
functor WBTree(Node : ORD) =
struct
   datatype t = E
              | T of int * Node.t * t * t;

   val empty = E;
   
   fun singleton (v : Node.t) = T (1, v, E, E);

   fun size E = 0
     | size (T (n, _, _, _)) = n;

   fun bin x l r = T (1 + size l + size r, x, l, r);
   (* more to come *)
end;

1.3.1. Desired API

We will want some "public" functions for a weight-balanced tree:

empty : t for publicly using the empty tree
singleton : Node.t -> t for public constructing a tree consisting of a single node
size : t -> int tells us how many nodes are in the tree;
null : t -> bool tests if a tree is empty;
insert : Node.t -> t -> t takes a value and a tree, then produce a tree with the value inserted into it;
member : Node.t -> t -> bool checks if a value belongs to a tree or not;
delete : Node.t -> t -> t removes a value from a tree (if present), or does nothing (if absent).

There are some "nice to have" functions, which "working programmers" will want…but we may or may not need all of them:

Set operations on two trees
- union : t -> t -> t which will add elements from the second tree (the "right" tree) to the first "left" tree if the element is absent from the first tree — so if the comparison of node values is not injective (intuitively: two distinct values are "equivalent" and treated as EQUAL), then the existing value is kept.
- difference : t -> t -> t which will remove elements from the first tree which are present in the second tree
- intersection : t -> t -> t which will produce a tree consisting of values from the first tree which are members of the second tree.
List conversions
- toList : t -> Node.t list converts a weight-balanced tree into a [sorted] list
- fromList : Node.t list -> t converts a list into a weight-balanced tree
Reducing a tree into a value by applying a function iteratively
- foldl : (Node.t -> 'a -> 'a) -> 'a -> t -> 'a left reduces the tree in ascending order, i.e., it's the same as foldl f b t = List.foldl f b (toList t)
- foldr : (Node.t -> 'a -> 'a) -> 'a -> t -> 'a right reduces the tree in ascending order, i.e., it's the same as foldr f b t = List.foldr f b (toList t)
Predicates and quantifiers
- eq : t * t -> bool tests if all the elements in one tree is in the other tree.
- filter : (Node.t -> bool) -> t -> t constructs a new tree consisting of all the elements which satisfy the predicate.
- exists : (Node.t -> bool) -> t -> bool tests each element of the tree, and returns true upon the first success (or false upon universal failure).
- all : (Node.t -> bool) -> t -> bool tests every element of the tree against the supplied predicate, returns false upon first failure (or true upon universal success).
Debugging
- showTree : (Node.t -> string) -> t -> string produces a string representation of the tree.
- isValid : t -> bool testing if the tree is actually a valid weight-balanced tre.

The only "obvious" function which would be nice to have, but is not at all obvious how to implement it, would be a map : (Node.t -> 'a) -> t -> 'a Tree? There is probably a way to do it, but I cannot see it at present. However, we can construct a app : (Node.t -> unit) -> t -> unit function which will apply a function yielding side-effects to each node in the tree.

1.4. "Balanced" part of "Weight-Balanced Tree"

Our intuition is that we have a binary tree consist of a left subtree \(L\) and a right subtree \(R\), we think they are balanced if the size of the right subtree \(|R|\) is bounded by a multiple of the size of the left subtree. i.e., \(\Delta\cdot|L|\geq|R|\) and a similar condition for the left subtree \(\Delta\cdot|R|\geq|L|\) for some fixed real constant \(\Delta\geq1\) (usually \(\Delta\in\{2,3,4\}\)). There is some subtlety when \(|R|=0\) or \(|L|=0\), when we should allow the other subtree to be either empty or a singleton. Formally:

Let Delta be a positive number. We say a weight-balanced tree \((n, x, L, R)\) is Strictly Balanced if:

When the subtrees L and R are both non-empty: Delta*size(L) > size(R) and Delta*size(R) > size(L);
If either subtree is empty, the other is either a singleton or empty.

We say a weight-balanced tree is Balanced if

Delta*(1 + size(L)) >= 1 + size(R) and
Delta*(1 + size(R)) >= 1 + size(L).

Observe, if a weight-balanced tree is "strictly balanced", then it is also "balanced".

The use of Delta allows some "wiggle room" in determining if a tree is balanced. The larger the Delta, the fewer times we demand the tree be rebalanced; on the other hand, the smaller the value of Delta, the more "perfectly" balanced the tree becomes (and the quicker it is to perform operations).

For example, when Delta is 2, and size(L) = 5, then a strictly balanced tree allows the range of sizes 10 > size(R) >= 3 for the right subtree.

When Delta is 3 and size(L) = 5, then a strictly balanced tree allows 15 > size(R) >= 2 for the sizes for the right subtree.

There is some slight variation in the definition of a WBT being balanced. For example, Hirai and Yamamoto define it as Delta*(size(R) + 1) >= size(L) + 1 and Delta*(size(L) + 1) >= size(R) + 1. This is a slightly more generous condition; instead of Delta*size(L) > size(R) >= ceiling(size(L)/Delta), we would allow Delta*size(L) + (Delta - 1) >= size(R) >= ceiling(size(L)/Delta) - 1.

We will conceptually think of subtree \(T_{1}\) as Balanced With Respect to subtree \(T_{2}\) if \(\Delta\cdot(|T_{2}|+1)\geq|T_{1}|+1\). This is implemented as isBalanced T2 T1 — the intuition is the curried form isBalanced T2 is a predicate testing if its argument (the expected \(T_{1}\)) is balanced with respect to \(T_{2}\).

Then the assertion that the tree as a whole is balanced is then balanced T and implemented in terms of checking if the left and right subtrees are balanced with respect to each other (and if they are, themselves, balanced trees). We could implement this predicate in Standard ML as:

(* wbtree.fun *)
functor WBTree(Node : ORD) =
struct
   datatype t = E | T of int * Node.t * t * t;

   val empty = E;
   fun singleton (v : Node.t) = T (1, v, E, E);

   fun size E = 0
     | size (T (n, _, _, _)) = n;

   val delta : int = 3;

   (* isBalanced : t -> t -> bool *)
   fun isBalanced l r = delta*(size l + 1) >= (size r + 1);

   fun balanced E = true
     | balanced (T (_, _, l, r)) = isBalanced l r andalso
                                   isBalanced r l andalso
                                   balanced l andalso balanced r;
   (* more to come *)
end;

2. Inserting a new value

Constraint: values found in the left subtree are less than the value of the root node, and values found in the right subtree are greater than the value of the root node. We will refer to this condition as the Ordering Constraint. (End of constraint)

Suppose we had a tree of integers. Let us try maintaining the ordering constraint with the implementation:

(* first attempt *)
fun insert x E = singleton x
  | insert x (t as T (sz, v, l, r)) =
    case compare(x,v) of
       LESS => T (sz + 1, v, insert x l, r)
     | EQUAL => t
     | GREATER T(sz + 1, v, l, insert x r);

This obeys our demand: every element of the right subtree is greater than the root of the subtree, and every element of the left subtree is less than the root of the subtree. But what happens with foldr (fn (x,tree) => insert x tree) E [1,2,3,4,5]? Well, we get T(5,1,E, T(4,2,E, T(3,3,E, T(2,4,E, T(1, 5, E, E))))). Or, graphically:

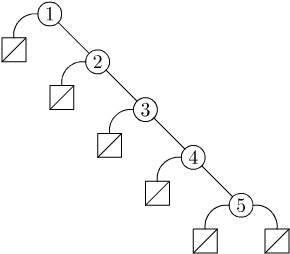
Figure 1: Naive insertion of [1,2,3,4,5] into an empty tree.

This is just a linked list with extra baggage! How can we fix this situation?

Well, the astute reader will note our insert function does not check if the subtrees are balanced. Therefore, why on Earth would anyone expect the result to be a balanced tree?

2.1. Observation: Many Trees Exist for the Same Set of Values

The "killer insight" which will help us remedy our problem (the tree is out of balance after insertion) is to realize that given some finite set of values, there are many different possible trees whose nodes are precisely our finite set.

To see this, observe the following two trees:

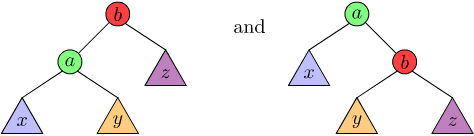
Figure 2: Two possible weight-balanced trees with \(x < a < y < b < z\).

They both obey the ordering constraint. The trick is to check, after insertion, if the subtree receiving the new node is "too heavy" and to transform it into an equivalent-but-balanced tree.

2.2. Tree Rotations

We can remedy this by balancing the tree after inserting a new node:

(* insert : Node.t -> t -> t *)
fun insert x E = singleton x
  | insert x (tree as T (sz, v, l, r)) =
    case compare(x,v) of
       LESS => balanceL v (insert x l) r
     | EQUAL => tree
     | GREATER => balanceR v l  (insert x r);

We call balanceL when inserting a new element into the left subtree (or deleting something from the right subtree), which will guarantee the resulting left subtree is "not too big" (i.e., balanced). The function amounts to:

check if the tree constructed from the new left and right subtrees would be balanced;
- if so, then just construct the tree;
- otherwise move a branch of the left subtree over to the right subtree (computer scientists call this: rotating right "by some amount").

Similarly, balanceR is invoked to make sure the right subtree is "not too big" and will restore balance by rotating left.

This is a classic trick with binary trees: rotations to rebalance them. Tree rotation can graphically visualized as:

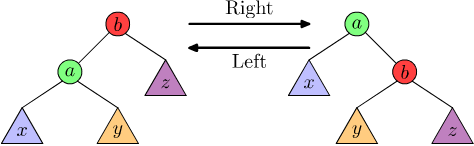
Figure 3: Single left and single right rotations of tree with \(x < a < y < b < z\).

We see that size r > delta*(size l) is the same as not isBalanced l r, i.e., the right subtree is "too big" when isBalanced l r is false. Similarly, size l > delta*(size r) is the same as not isBalanced r l, which tells us the left subtree is "too big".

There is an edge-case worth discussing: what if we start with a tree like in the left-hand side of figure 3, where the left subtree is too heavy, so we rotate…but then after rotation, the right subtree is too heavy? We would be shifting the \(y\) subtree back and forth in an infinite loop. Could this happen?

The initial tree having its left subtree too heavy corresponds to the condition:

\begin{equation} 1 + (1 + |LL| + |LR|) > \Delta(1 + |R|). \end{equation}

The post-rotation right subtree being too heavy corresponds to the condition:

\begin{equation} 1 + (1 + |R| + |LR|) > \Delta(1 + |LL|). \end{equation}

Our intuition should be that the \(|LR|\) subtree (the \(y\) subtree in the figure) is "too heavy". We can formalize this intuition as something like:

\begin{equation} |LR| \geq\alpha|LL| \end{equation}

for some \(\alpha\geq1\). If we write

\begin{equation} |R| = |LL| + \delta r \end{equation}

for some \(\delta r\in\mathbb{Z}\), then we have

\begin{equation} 1 + (1 + |LL| + \delta r + |LR|) > \Delta(1 + |LL|), \end{equation}

hence

\begin{equation} 1 + |LR| + \delta r> (\Delta - 1)(1 + |LL|). \end{equation}

Since we want this to be true for arbitrary weight-balanced trees, the condition becomes

\begin{equation} 1 + |LR| \geq (\Delta - 1)(1 + |LL|), \end{equation}

hence

\begin{equation} \alpha = \Delta - 1. \end{equation}

(We encode \(\alpha\) as ratio in our Standard ML code.) In this case, the "innermost" subtree is "too heavy", and we will keep switching it back and forth.

For this particular situation, we need to "break up" the \(y\) subtree before moving things around. Computer scientists call this a "double rotation". A double left rotation moves a "pivot" node "from the left" by two positions. Graphically:

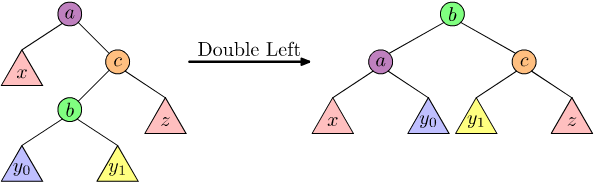
Figure 4: Double left rotation of tree with \(x < a < y_{0} < b < y_{1} < c < z\).

This is done first by performing a "local right" rotation:

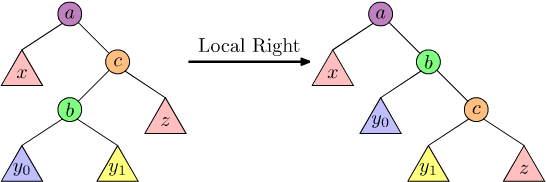
Figure 5: "Local right" rotation of tree with \(x < a < y_{0} < b < y_{1} < c < z\).

Then a "global left" rotation yields the result. We can similarly construct a double right rotation as moving a "pivot" node "from the right" by two positions.

2.3. Implementation

The implementation of this, albeit unoptimized:

(* balanceR : Node.t -> t -> t -> t *)
fun balanceR x l r = if isBalanced l r
                     then bin x l r
                     else (* when size r > delta*(size l) *) rotateL x l r;

(* balanceL : Node.t -> t -> t -> t *)
fun balanceL x l r = if isBalanced r l
                     then bin x l r
                     else (* when size l > delta*(size r) *) rotateR x l r;

Now it's just a matter to code up left rotations, right? Well, we also have double rotations.

(* rotateL : Node.t -> t -> t -> t *)
fun rotateL x l (r as (T (_, _, rl, rr))) =
    if isSingle rl rr then singleL x l r
    else doubleL x l r
  | rotateL _ _ _ = raise "rotateL";

fun singleL x l (T (_, v, rl, rr)) = bin y (bin x l rl) rr
  | singleL _ _ _ = raise "singleL";

fun doubleL x l (T (_, y, (T (_, z, rll, rlr)), rr))
    = bin z (bin x l rll) (bin y rlr rr)
  | doubleL _ _ _ = raise "doubleL";

(* ...and analogous functions for right rotations *)

But what is the condition for isSingle? Basically, if the ratio of the size of the left subtree to the size of the right subtree is less than the alpha parameter used in the previous subsection when deriving double rotations. For us, we name alpha something more relevant, ratio, and this condition becomes:

(* isSingle : t -> t -> bool *)
fun isSingle l r = (size l + 1) < ratio*(size r + 1);

Thanks to the work of Hirai and Yamamoto, we know that delta = 3 and ratio = 2 are the only integer solutions, so we pick those values. We combine these functions together, and our functor so far becomes:

(* wbtree.fun *)
functor WBTree(Node : ORD) =
struct
   datatype t = E | T of int * Node.t * t * t;

   val empty = E;
   fun singleton (v : Node.t) = T (1, v, E, E);

   fun size E = 0
     | size (T (n, _, _, _)) = n;

   fun bin x l r = T(1 + size l + size r, x, l, r);

   (* laziness *)
   val compare = Node.compare;

   val ratio : int = 2;
   val delta : int = 3;

   (* isBalanced : t -> t -> bool *)
   fun isBalanced l r = delta*(size l + 1) >= (size r + 1);

   fun balanced E = true
     | balanced (T (_, _, l, r)) = isBalanced l r andalso
                                   isBalanced r l andalso
                                   balanced l andalso balanced r;

   (* Helper functions to ensure the tree isBalanced *)
   fun isSingle a b = (size a + 1) < ratio*(size b + 1);

   fun singleL x l (T (_, y, rl, rr)) = bin y (bin x l rl) rr
     | singleL _ _ _ = raise (Fail "singleL");

   fun doubleL x l (T (_, y, (T (_, z, rll, rlr)), rr))
       = bin z (bin x l rll) (bin y rlr rr)
     | doubleL _ _ _ = raise (Fail "doubleL");

   fun singleR x (T (_, y, ll, lr)) r = bin y ll (bin x lr r)
     | singleR _ _ _ = raise (Fail "singleR");

   fun doubleR z (T (_, x, ll, (T (_, y, lrl, lrr)))) r
       = bin y (bin x ll lrl) (bin z lrr r)
     | doubleR _ _ _ = raise (Fail "doubleR");

   fun rotateR x (l as (T (_, _, ll, lr))) r =
       if isSingle lr ll then singleR x l r
       else doubleR x l r
     | rotateR _ _ _ = raise (Fail "rotateR");

   fun rotateL x l (r as (T (_, _, rl, rr))) =
       if isSingle rl rr then singleL x l r
       else doubleL x l r
     | rotateL _ _ _ = raise (Fail "rotateL");

   fun balanceR x l r = if isBalanced l r then bin x l r
                        else rotateL x l r;

   fun balanceL x l r = if isBalanced r l then bin x l r
                        else rotateR x l r;

   (* insert : Node.t -> t -> t *)
   fun insert x E = singleton x
     | insert x (tree as T (sz, v, l, r)) =
       (case compare(x,v) of
           LESS => balanceL v (insert x l) r
         | EQUAL => tree
         | GREATER => balanceR v l  (insert x r));
   (* more to come *)
end;

Assume l and r are balanced trees, and x is a value such that it lies between the subtrees.

Prove balanceL x l r produces a balanced tree.
Prove balanceR x l r produces a balanced tree.

Assume l and r are balanced trees and x is a value that lies between the two trees. What is the worst-case, best-case, and average runtime complexities of balanceL x l r? Is the runtime complexities for balanceR x l r the same?

Optimize our code. We proved it works (well, in an exercise), so prove your optimizations "work" as well!

There are many different avenues for optimization, for example: balanceL and balanceR recursively call functions which destruct the arguments in the same way; is it faster to "collapse" the helper rotate functions into one giant balanceL (and another giant balanceR) function?

For other ideas, see Milan Straka's "The performance of the Haskell Containers Package" (2010).

Prove or find a counter-example: insert is not commutative, in the sense that for any tree t and any values x and y, we do not have insert x (insert y t) identical as a tree to insert y (insert x t). The two trees have the same set of nodes, but the branches are different.

3. Querying for an Element

How can we check if a tree \(T\) contains an element \(x\)? There are two cases:

If \(T\) is empty, then \(x\) is not a member of it; and
If \(T\) is not empty, then we can write \(T = (n,y,L,R)\). We should compare \(x\) against \(y\) (the value for the node in the branch). If they are equal, then \(x=y\) and \(x\) is a member of the tree.

If \(x < y\), then we should recursively check the subtree \(L\) to see if \(x\) is a member of \(L\).

If \(x > y\), then we should recursively check the right subtree \(R\) to see if \(x\) is a member of \(R\).

Since the subtrees \(L\) and \(R\) are balanced, there would be about \(\log_{2}(n)\) iterations when searching if \(x\) is a member of the tree. We can easily code this up as:

functor WBTree(Node : ORD) =
struct
   (* ... *)

   (* member : Node.t -> t -> bool *)
   fun member x E = false
     | member x (T (_,y,l,r)) = case compare(x,y) of
                                    EQUAL => true
                                  | LESS => member x l
                                  | GREATER => member x r;

   (* ... *)
end;

Write a function to query for the subtree consisting of elements:

less than or equal to \(x\)
strictly less than \(x\)
greater than or equal to \(x\)
strictly greater than \(x\)

4. Deleting an Element

When deleting an element from a weight-balanced tree, we just need to do the mirror image of an insertion (e.g., when deleting a value from the left subtree, we need to invoke balanceR). The only tricky bit is what happens when we want to delete the value at the root of the tree. Uh, well, we'll just brush that problem into another function which will glue the subtrees into a new weight-balanced tree.

(* delete : Node.t -> t -> t *)
fun delete _ E = E
  | delete x (tree as T (_, y, l, r)) =
    (case compare (x,y) of
         LESS => balanceR y (delete x l) r
       | EQUAL => glue l r
       | GREATER => balanceL y l (delete x r));

Now, how do we glue two weight-balanced trees together? There are some simple cases: if l is empty, just return the right subtree; if r is empty, return the left subtree.

When both l and r are non-empty, we have two possibilities:

When size l > size r, then take the largest value found in the left subtree l, then surgically remove it from l to obtain the value m and the lobotomized left subtree l' and then (since the right subtree may be too big) we rebalance everything by invoking balanceR m l' r to produce a balanced tree;
Otherwise, we do the mirror image of everything we did in the previous case, except we surgically remove the smallest value from the right subtree to obtain the value m and the lobotomized right subtree r' and rebalance everything by invoking balanceL m l r' to produce a balanced tree.

(* glue : t -> t -> t *)
fun glue E r = r
  | glue l E = l
  | glue (l as T(sl, xl, ll, lr)) (r as T(sr, xr, rl, rr))
    = if sl > sr then (let val (m, l') = maxViewSure xl ll lr
                       in balanceR m l' r
                       end)
      else (let val (m, r') = minViewSure xr rl rr
            in balanceL m l r'
            end);

We can get the maximum element of a tree, plus a version of the tree with that element removed. How? Simply plumb the right subtree — recursively examine the right subtree until it is finally empty, then the node must contain the maximum value. Since we assume the tree is balanced, we know that every value in the left subtree will be less than any value in the right subtree.

We will return the rebalanced right-subtree (minus the maximum value) and the maximum value:

(* maxViewSure : Node.t -> t -> t -> Node.t * t *)
fun maxViewSure x l E = (x, l)
  | maxViewSure x l (T (_, xr, lr, rr)) =
    (case maxViewSure xr lr rr of
         (m, r') => (m, balanceL x l r'));

(* maxView : t -> (Node.t * t) option *)
fun maxView E = NONE
  | maxView (T (_, x, l, r)) = SOME (maxViewSure x l r);

Similarly, the minimum element of the tree, and a version of the tree with that element surgically removed. How? Well, we just keep examining the left sub-tree until we find the smallest element. Since the tree is assumed to be balanced, we know the left subtree consists of values guaranteed to be smaller than any value found in the right subtree. So we just surgically remove the smallest element, then rebalance the remaining trees:

(* minViewSure : Node.t -> t -> t -> Node.t * t *)
fun minViewSure x E r = (x, r)
  | minViewSure x (T (_, xl, ll, lr)) r =
    (case minViewSure xl ll lr of
         (m, l') => (m, balanceR x l' r));

(* minView : t -> (Node.t * t) option *)
fun minView E = NONE
  | minView (T (_, x, l, r)) = SOME (minViewSure x l r);

Great, now we have the ability to insert and delete elements from our weight-balanced tree.

Prove, if tree is a balanced weight-balanced tree containing the value x, then delete x tree produces a balanced weight-balanced tree.

Change our code for the case when x is not contained in tree, then we have delete x tree return the tree unmodified.

[Hint: we cannot use equality directly to write something like tree = delete x tree, but we know the size of the tree before and after deletion will be the same if and only if they are the same. Well, you should prove the size would be the same before and after deletion iff no delete occurred.]

In summary, the code related to the delete function is collected thus:

functor WBTree(Node : ORD) =
struct
   (* ... *)
   (** Helper functions for delete **)
   (* Retrieve the maximal key for the set, and the set stripped
      of that element. *)
   fun maxViewSure x l E = (x, l)
     | maxViewSure x l (T (_, xr, lr, rr)) =
       (case maxViewSure xr lr rr of
            (m, r') => (m, balanceL x l r'));

   fun maxView E = NONE
     | maxView (T (_, x, l, r)) = SOME (maxViewSure x l r);

   fun minViewSure x E r = (x, r)
     | minViewSure x (T (_, xl, ll, lr)) r =
       (case minViewSure xl ll lr of
            (m, l') => (m, balanceR x l' r));

   (* Retrieves the minimal key of the set, and the set is stripped of that
      element, or `NONE` if passed an empty list. *)
   fun minView E = NONE
     | minView (T (_, x, l, r)) = SOME (minViewSure x l r);

   (* Glue two trees together.
      Assume that `l` and `r` are already balanced with respect to each
      other. *)
   fun glue E r = r
     | glue l E = l
     | glue (l as T(sl, xl, ll, lr)) (r as T(sr, xr, rl, rr))
       = if sl > sr then (let val (m, l') = maxViewSure xl ll lr
                          in balanceR m l' r
                          end)
         else let val (m, r') = minViewSure xr rl rr
              in balanceL m l r'
              end;

   (* delete : Node.t -> t -> t *)
   fun delete _ E = E
     | delete x (tree as T (_, y, l, r)) =
       (case compare (x,y) of
            LESS => balanceR y (delete x l) r
          | EQUAL => glue l r
          | GREATER => balanceL y l (delete x r));

   (* more to come *)
end;

5. Appendix: Source Code by Files

5.1. ord.sig

(* ord.sig *)

(* minimal signature which is fleshed out in a functor *)
signature COMPARABLE =
sig
    type t;
    val compare : t * t -> order;
end;

signature ORD =
sig
    type t;
    val compare : t * t -> order;
    val gt : t * t -> bool;
    val eq : t * t -> bool;
    val lt : t * t -> bool;
    val geq : t * t -> bool;
    val leq : t * t -> bool;
    val max : t * t -> t;
    val min : t * t -> t;
end;

functor Ord(Ordered : COMPARABLE) : ORD with type t = Ordered.t =
struct
    type t = Ordered.t;
    val compare = Ordered.compare;
    fun gt (x,y) = compare (x,y) = GREATER;
    fun eq (x,y) = compare (x,y) = EQUAL;
    fun lt (x,y) = compare (x,y) = LESS;
    fun geq (x,y) = not (lt (x,y));
    fun leq (x,y) = not (gt (x,y));
    fun max (x,y) = if lt(x,y) then y else x;
    fun min (x,y) = if lt(x,y) then x else y;
end;

5.2. wbtree.fun

functor WBTree(Node : ORD) =
struct
   datatype t = E | T of int * Node.t * t * t;

   val empty = E;
   fun singleton (v : Node.t) = T (1, v, E, E);

   fun size E = 0
     | size (T (n, _, _, _)) = n;

   fun bin x l r = T(1 + size l + size r, x, l, r);

   (* laziness *)
   val compare = Node.compare;

   val ratio : int = 2;
   val delta : int = 3;

   (* member : Node.t -> t -> bool *)
   fun member x E = false
     | member x (T (_,y,l,r)) = case compare(x,y) of
                                    EQUAL => true
                                  | LESS => member x l
                                  | GREATER => member x r;

   (* isBalanced : t -> t -> bool *)
   fun isBalanced l r = delta*(size l + 1) >= (size r + 1);

   fun balanced E = true
     | balanced (T (_, _, l, r)) = isBalanced l r andalso
                                   isBalanced r l andalso
                                   balanced l andalso balanced r;

   (* Helper functions to ensure the tree isBalanced *)
   fun isSingle a b = (size a + 1) < ratio*(size b + 1);

   fun singleL x l (T (_, y, rl, rr)) = bin y (bin x l rl) rr
     | singleL _ _ _ = raise (Fail "singleL");

   fun doubleL x l (T (_, y, (T (_, z, rll, rlr)), rr))
       = bin z (bin x l rll) (bin y rlr rr)
     | doubleL _ _ _ = raise (Fail "doubleL");

   fun singleR x (T (_, y, ll, lr)) r = bin y ll (bin x lr r)
     | singleR _ _ _ = raise (Fail "singleR");

   fun doubleR z (T (_, x, ll, (T (_, y, lrl, lrr)))) r
       = bin y (bin x ll lrl) (bin z lrr r)
     | doubleR _ _ _ = raise (Fail "doubleR");

   fun rotateR x (l as (T (_, _, ll, lr))) r =
       if isSingle lr ll then singleR x l r
       else doubleR x l r
     | rotateR _ _ _ = raise (Fail "rotateR");

   fun rotateL x l (r as (T (_, _, rl, rr))) =
       if isSingle rl rr then singleL x l r
       else doubleL x l r
     | rotateL _ _ _ = raise (Fail "rotateL");


   fun balanceR x l r = if isBalanced l r then bin x l r
                        else rotateL x l r;

   fun balanceL x l r = if isBalanced r l then bin x l r
                        else rotateR x l r;

   (* insert : Node.t -> t -> t *)
   fun insert x E = singleton x
     | insert x (tree as T (sz, v, l, r)) =
       (case compare(x,v) of
           LESS => balanceL v (insert x l) r
         | EQUAL => tree
         | GREATER => balanceR v l  (insert x r));

   (** Helper functions for delete **)
   (* Retrieve the maximal key for the set, and the set stripped
      of that element. *)
   fun maxViewSure x l E = (x, l)
     | maxViewSure x l (T (_, xr, lr, rr)) =
       (case maxViewSure xr lr rr of
            (m, r') => (m, balanceL x l r'));

   fun maxView E = NONE
     | maxView (T (_, x, l, r)) = SOME (maxViewSure x l r);

   fun minViewSure x E r = (x, r)
     | minViewSure x (T (_, xl, ll, lr)) r =
       (case minViewSure xl ll lr of
            (m, l') => (m, balanceR x l' r));

   (* Retrieves the minimal key of the set, and the set is stripped of that
      element, or `NONE` if passed an empty list. *)
   fun minView E = NONE
     | minView (T (_, x, l, r)) = SOME (minViewSure x l r);

   (* Glue two trees together.
      Assume that `l` and `r` are already balanced with respect to each
      other. *)
   fun glue E r = r
     | glue l E = l
     | glue (l as T(sl, xl, ll, lr)) (r as T(sr, xr, rl, rr))
       = if sl > sr then (let val (m, l') = maxViewSure xl ll lr
                          in balanceR m l' r
                          end)
         else let val (m, r') = minViewSure xr rl rr
              in balanceL m l r'
              end;

   (* delete : Node.t -> t -> t *)
   fun delete _ E = E
     | delete x (tree as T (_, y, l, r)) =
       (case compare (x,y) of
            LESS => balanceR y (delete x l) r
          | EQUAL => glue l r
          | GREATER => balanceL y l (delete x r));

   (* more to come *)
end;

6. References

Jürg Nievergelt and Edward M. Reingold,
"Binary search trees of bounded balance".
STOC '72: Proceedings of the fourth annual ACM symposium on Theory of computing, May 1972, Pages 137–142 https://doi.org/10.1145/800152.804906
- Cited/blamed as the origin/inspiration for weighted-balanced trees
Stephen Adams,
"Functional Pearls: Efficient sets — a balancing act".
In J. of Func. Progr. 3 no.4 (1993) pp.553–561, Eprint
Yoichi Hirai and Kazuhiko Yamamoto,
"Balancing weight-balanced trees".
Journal of Functional Programming 21 no.3 (2011) 287–307. PDF
- CAUTION: the balanceL and balanceR functions described by Hirai and Yamamoto are the opposite of their definitions in Haskell (and we follow the definitions of Haskell).
Lukas Barth and Dorothea Wagner,
"Engineering Top-Down Weight-Balanced Trees".
arXiv:1910.07849, 14 pages.
Joachim Breitner, Antal Spector-Zabusky, Yao Li, Christine Rizkallah, John Wiegley, Stephanie Weirich,
"Ready, Set, Verify! Applying hs-to-coq to real-world Haskell code".
arXiv:1803.06960, 30 pages.