Verifying Hardware with Isabelle/HOL

by Alex Nelson, 1 March 2024

There are several ways to formalize hardware in a proof assistant. I’m interested in how to do it with Isabelle/HOL, but I’m sure it’s not too hard to make it work in another proof assistant.

The basic strategy is to formalize a hardware implementation using NAND gates, formalize the machine language as an abstract machine, then prove every program in machine code evaluates “the same way” on both machines.

I have formalized the combinational circuitry of a simple ALU in Isabelle/HOL, and these are some notes about the basic ideas how we formalize computer hardware.

Electrical Engineering for Mathematicians in 5 minutes

The basic quantity of interest is voltage. We model boolean functions using electronic devices, we use voltage as the physical quantity encoding “true” and “false”, and wires carry voltage.

Aside. Although “high” voltage encodes “true”, and “low” voltage encodes “false”, there is also a “floating” voltage [denoted “Z”] which occurs when the voltage level changes, or other similar situations. For now, we may ignore “floating” voltage as an idealization similar to massless pulleys, or frictionless planes in physics. (End of aside)

The basic building blocks are transistors, which might be idealized as switches. A transistor can be connected to three wires called:

  1. the gate (which determines if the switch is “open” or “closed”, i.e., disconnects or connects the other two wires together)
  2. the source
  3. the drain

There are two kinds of transistors, P-type transistors connect the source and drain when the gate’s voltage is low, and N-type transistors connect them when the gate’s voltage is high.

The only other basic building blocks are the power source, which connects to one wire and supplies “high” voltage; and the ground, which connects to one wire, and “supplies” low voltage.

We then can wire together these four building blocks (P-transistors, N-transistors, power, and ground) to form an electronic device. Usually there is only one source and one ground in most schematics.

For combinational circuits, we can work mentally with voltages and ignore time. It’s only when we get to sequential circuits that time becomes important.

In effect, the mental model should be that wires are functions from time (usually $\mathbb{N}_{0}$ the non-negative integers) to voltage $\{0,1\}$.

Aside 2. We might wonder if these are adequate idealizations, and they get us a lot of mileage. We might improve our discussion by introducing capacitors, modeling a transistor as a capacitor coupled to a switch, and so on. We might expand the description of voltage from $\{0,1\}$ to $\{0,1,X,Z\}$ to include “don’t care” $X$ as well as “floating/high-impedence” $Z$, or even something more sophisticated. We can do all these things, but we hit diminishing returns for exploring hardware. If we were hired by, say, Intel, then we would almost certainly want to include such a degree of realism. (End of aside 2)

Logic Gates as Logical Relations

Historically, the first successful approach to formalizing real world hardware was Anthony Fox’s formalization of ARM 6 in HOL. Fox’s ingenuity boils down to the slogan: “A logic gate is a logical relation of its inputs and outputs”. (To be fair, Mike Gordon realized this in the 1980s, see the bibliography for references, but Fox was the first to formalize an actual CPU.)

Recall that a function $f\colon X\to Y$ is also a binary relation $f\subset X\times Y$ with the property for each $x\in X$ there exists a unique $y\in Y$ such that $f(x)=y$…or, if you prefer treating it like a relation, $(x,y)\in f$. We can model the basic building blocks as functions, or we can model them as relations, it doesn’t matter at this stage of the game.

For example, the switch model of CMOS has:

definition PTran :: "bool × 'a × 'a ⇒ bool" where
  "PTran = (λ(g,a,b). (~g --> a = b))"

definition NTran :: "bool × 'a × 'a ⇒ bool" where
  "NTran = (λ(g,a,b). (g --> a = b))"
  
definition Power :: "bool ⇒ bool" where
  "Power p = (p = True)"

definition Ground :: "bool ⇒ bool" where
  "Ground p = (p = False)"

This is so general that we could allow PTran to work on signals a and b, or on whatever we’d want.

We combine circuits L[in, out] and R[in, out] by EX x. L[in, x] ∧ R[x, out]. That is to say, we have a wire x which connects the output of L to the input of R, and this is modeled as yet another logical relation. This produces a third circuit C[in, out] modeled as a logical relation of signals.

Remark. There is nothing specifically forcing us to use higher-order logic. We could have ostensibly used first-order logic, formalizing CMOS circuits in Mizar for example. But Isabelle/HOL is the industry standard. (End of Remark)

This compositionality allows us to prove properties concerning constituent components, and use them to deduce results concerning the larger module.

Example 1. Here’s an example implementing a NAND gate using P-mos and N-mos transistors, with simple boolean-valued wires:

definition "PTran = (λ(g,a,b). (g ∧ ~b) ∨ (~g ∧ (a = b)))"

definition "NTran = (λ(g,a,b). (~g ∧ ~b) ∨ (g ∧ (a = b)))"

definition "Power p ≡ (p = True)"

definition "Ground p ≡ (p = False)"

definition "Join ≡ (λ(i1,i2,out). (out = (i1 ∨ i2)))"

definition 
 "NAND a b out ≡ EX w1 w2 w3 w4 w5 w6 w7.
    Power(w1) ∧
    PTran (a, w1, w2) ∧
    PTran (b, w1, w3) ∧
    Join(w2,w3,w4) ∧
    Join(w4,w5,out) ∧
    NTran(a, w6, w5) ∧
    NTran(b, w7, w6) ∧
    Ground(w7)"

We should then prove our NAND gate implementation with CMOS transistors works, which is a simple enough proof by cases followed by unfolding the definitions and brute-force:

lemma "NAND a b out <--> (out <--> ¬(a ∧ b))"
  apply (case_tac a; case_tac b)
  apply (simp add: NAND_def PTran_def NTran_def Ground_def Power_def Join_def; fastforce)+
  done

Example 2. I’ve been working with simple models of circuits as Boolean constants, but we could use signals and wires, writing something like:

type_synonym time = nat
type_synonym voltage = bool
type_synonym wire = "time ⇒ voltage"

definition Low :: ‹voltage ⇒ bool› where
"Low v = (v = True)"

definition High :: ‹voltage ⇒ bool› where
"High v = (v = False)"

definition "PTran = (λ(g,a,b). ∀t. ((High (g t) ∧ Low (b t)) ∨ (Low (g t) ∧ (a t = b t))))"

definition "NTran = (λ(g,a,b). ∀t. ((Low (g t) ∧ Low (b t)) ∨ (High (g t) ∧ (a t = b t))))"

definition "Power p ≡ ∀t. High (p t)"

definition "Ground p ≡ ∀t. Low (p t)"

definition Join :: "wire * wire * wire ⇒ bool" where
  "Join ≡ (λ(i1,i2,out). ∀t. ((out t) = max (i1 t) (i2 t)))"

Example 3. Or if we wanted to measure the actual voltage, we could do something like:

type_synonym time = nat
type_synonym voltage = nat
type_synonym wire = "time ⇒ voltage"

definition Low :: ‹voltage ⇒ bool› where
"Low v = (v = 0)"

definition High :: ‹voltage ⇒ bool› where
"High v = (¬(v = 0))"

definition "PTran = (λ(g,a,b). ∀t. ((High (g t) ∧ Low (b t)) ∨ (Low (g t) ∧ (a t = b t))))"

definition "NTran = (λ(g,a,b). ∀t. ((Low (g t) ∧ Low (b t)) ∨ (High (g t) ∧ (a t = b t))))"

definition "Power p ≡ ∀t. High (p t)"

definition "Ground p ≡ ∀t. Low (p t)"

definition 
  "Join ≡ (λ(i1,i2,out). ∀t. ((out t) = max (i1 t) (i2 t)))"

The definition of NAND a b out remains the same in either case, amazingly enough. Proving that the defining property of NAND is satisfied by this implementation is much more difficult. One way is simple:

lemma NAND_impl_implies_spec: "NAND a b out -->
    (∀t. (High (out t) = (¬(High (a t) ∧ High (b t)))))"
  apply (simp add: NAND_def PTran_def NTran_def Ground_def Power_def Join_def)
  by (metis High_def Low_def max_nat.eq_neutr_iff)

The other way is nontrivial, and requires some clever lemmas.

But the illustration is clear: we compose these implementations together to get larger and larger units. This would allow us to model the entire CPU’s implementation, and we could prove that it satisfies some specification.

Combinational Circuits

We can take advantage, for combinational circuits only, of the fact that a logical relation L[in_1, ..., in_N, out] describes a function if for each different in_1, …, in_N there exists a unique value out. Combinational circuits (like NAND gates, half-adders, full adders, all the way up to the ALU) satisfy this property.

We could therefore describe combinational circuits using functions in HOL (and I did this!), rather than using logical relations. However, this fails to carry over for sequential circuits (like RAM, CPU registers, etc.). For sequential circuits, we must fall back on relying upon the usual strategy modeling them as logical relations.

Puzzle 1. Can we formalize a floating-point unit using Isabelle/HOL in a clear, pedagogically satisfying manner? Can we make it adhere to the IEEE-754 standard? Can we prove it adheres to the IEEE-754 Standard? (End of Puzzle 1)

Sequential Circuits

The motivating example of a sequential circuit is a diagram like the following: we have two inverters, which form a closed circuit. We would have something like the following diagram:

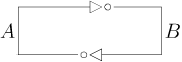
Image

If $A$ were high voltage, then $B=\overline{A}$ would be its negation and necessarily low voltage. If $A$ were low voltage, then $B$ would be high voltage.

We effectively have obtained a way to store 1 bit of information, and usually this is denoted by the letter $Q$, something like the following diagram:

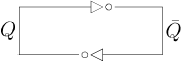
Image

In practice, we have a way to set $Q$ to a specific value, and a way to read the current value of $Q$. This gives us effectively a latch or a flip-flop.

Different implementations use different logic gates instead of inverters. Some use NOR gates, others use NAND. The basic schematic we have sketched underlies the gated D latex using pass transistor logic.

This also demonstrates why the “naive” approach using functions for circuits fails. I wouldn’t even know where to begin with such an approach. The predicate formalization is straightforward:

definition "D-gate q ≡ ex qBar. ∀t. (qBar (t + 1) = ¬(q t)
    ∧ q (t + 1) = ¬(qBar t))"

This is reasonable, but if we tried to make it a function?

References

For ARM6

Anthony Fox describes his work doing this for ARM 6 in a series of Technical Reports:

This approach allows us to formulate statements about sequential logic gates, since we’d just relate the output of the gate as out(t + 1) and relate it to the output from the previous time step out t as well as the other inputs at time t.